━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
課題b (構文木の生成 と 値の評価)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
●目標
算術式と論理式からなるプログラムを表す木構造を構築し，値を評価する．
●課題一覧
b1 構文木の基本操作
b2 構文木の生成
b3 式の評価
b4 リスト処理
b5 構文木の改良
●注意
実験時間内に課題が終わらない場合には，次回に持ち越さずに，
授業以外の時間を使って今回の課題を仕上げておく．
──────────────────────────────────────
●課題bの準備
課題に目を通して，
・式の木構造による表現
・木構造(2分木と多分木)のデータ構造とアルゴリズム
・式の評価の再帰関数
の解説に不明点があれば，自分で調査して基礎知識を事前に補っておく．
次のプログラムをコンパイル・実行し，2分木の構成方法や走査のアルゴリズム
について，自分の言葉で他人に説明できる程度に十分に理解する．
・bintree.c (2分木の生成と走査)
特に，課題bでは，複数の木を生成して利用できることが必須である．
構文木(プログラムを表す木構造)を生成して利用するには，
木構造のメモリ上の配置についてもよく理解する必要がある．
【参考】2分木のデータ構造については第2週の課題も参照．
言語処理系の作成は，すべて ~/proglang ディレクトリで実施する．
$ cd ~/proglang/
必要なら，前回作成したファイルの予備を作る．
$ cp -r ~/proglang ~/proglang-a
──────────────────────────────────────
●基本課題b1 (構文木の基本操作)
構文解析器は，プログラミング言語の文法に沿った木構造の中間データを
解析の結果として出力する．これを抽象構文木(abstract syntax tree)
あるいは単に構文木と呼ぶ．言語処理系で使われる構文木は，構文解析で
得られる解析木からプログラムの解析に不要な部分を取り除いて単純化した
ものを使うことが多い．
例えば，SS言語の二つの式 (* (+ x 1) 2) と (data ((a b c) () (d e)))
を表す構文木は，子の数に上限のない木(多分木)を使って次の形で表せる．
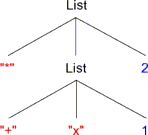
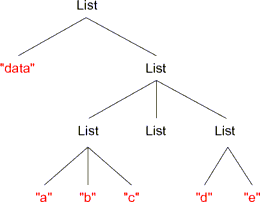この木を直接表現する多分木のデータ構造を定義してもよいが，この課題では，
リストが入れ子になった階層構造を，既に学んだ2分木を使って表す．
具体的な式に対応する2分木を，データ構造の模式図で表したものを，
次のファイルに示す．
SS言語の構文木の2分木による表現
まず，単独の数や名前や空リストは，2分木の一つの節で表す．課題bの準備で
扱った bintree.c では，節のデータが1種類なので単純だったが，構文木では，
節の種類(数・名前・リスト)を区別する必要がある点に注意する．
2分木のデータ構造を bintree.c の print_tree() や tree.c の show_tree()
の形式で表示すれば，数 123 は 123[#,#]，名前 x は "x"[#,#]，
空リスト () は List[#,#] と表せる．
空でないリストは，先頭を取り除いた残りを再びリストとして扱える
再帰的データ構造で表す．例えば，リスト (z) は List["z"[#,#],List[#,#]]，
リスト (y z) は List["y"[#,#],List["z"[#,#],List[#,#]]]，リスト (x y z)
は List["x"[#,#],List["y"[#,#],List["z"[#,#],List[#,#]]]] と表す．
つまり，リストを表す節の左の子はリストの先頭要素(head)を表し，右の子は
その先頭要素を取り除いた残り(rest)のリストを表す，と定めることで，
2分木でリストを表す．
さらに，入れ子になった式 (* (+ x 1) 2) は，部分式 (+ x 1) の木を
T = List["+"[#,#],List["x"[#,#],List[1[#,#],List[#,#]]]] とおけば，
T を使って List["*"[#,#],List[T,List[2[#,#],List[#,#]]]] と表せる．
この例では，式 (* (+ x 1) 2) を表すリストの先頭(head)は演算の名前 *
であり，先頭を取り除いた残り(rest)は二つの演算対象 (+ x 1) と 2
からなるリスト ((+ x 1) 2) である．
構文木を扱うための，以下のヘッダとプログラムのファイルを ~/proglang/ に
保存する．
・tree.h (構文木の基本操作のヘッダ)
・tree.c (構文木の基本操作のソース)
tree.h の関数群のうち，大部分は tree.c での実装が済んでいる．
ヘッダファイルで基本操作の概略を把握してから，ソースコードをよく読んで，
実装済みの関数の1ステップごとの動作が説明できる程度に，構文木の実装方法
（データ構造とその操作方法）を十分に理解する．
式の2分木による表現と実装方法を理解したら，tree.c での実装が未完成の
基本操作の関数 add_subtree(), num_subtree(), get_subtree() を完成させよ．
2分木の基本操作の例を図解したものを，次のファイルに示す．
2分木への要素の追加
実装方法は多数あるので，基本操作が実現できれば図の通りでなくても良い．
なお，実装した基本操作が正しく動くことの確認には，次のプログラム
ファイルを使い，Makefile は課題aのものを参考にして自作する．
・b1.c (構文木の基本操作の利用例)
さらに，式 (* (+ x 1) 2) を表す構文木を生成して，期待通りの結果が
得られるかを確かめよ．この式の構文木には子が三つあり，それぞれ
* と (+ x 1) と 2 を表す部分木となるはずである．
結果を確かめる際には，木の内部構造の show_tree() による表示と，
構文木に対応する式の文字列の print_tree() による表示の，両方を示すこと．
構文木の操作として有用な基本操作(木の削除や挿入など)が他にあれば，
今後，必要に応じて追加してもよい．その際は，ヘッダファイルにも
書き加えて仕様を明示すること．なお，動的に確保するメモリを適切に
管理して，不要になる記憶域を全て開放できることが望ましいが，
これを完全に実現するのは難度が高いので，基本課題としては要求しない．
興味があれば「ガーベジコレクション」について学ぶとよい．
●基本課題b2 (構文木の生成)
構文解析の処理を実現するための以下のヘッダとプログラムのファイルを
~/proglang/ に保存する．
・parser.h (構文木の基本操作のヘッダ)
・parser.c (構文木の基本操作のソース)
まず，課題a3で作成した(a4で改良した)構文解析関数 parse_expression() の
本体を parser.c にコピーする．字句の表示部分を削除して，tree.h の関数を
使った構文木の生成処理を追加することで，式の構文解析器を完成させよ．
つまり，parser.c にコピーした構文解析の関数内の，文法の右辺を解析する
各位置で，数や名前に対応する木の節を生成したり，式の空列を表す木を
生成してから部分式に対応する部分木の追加を繰り返したりする．
この課題では，課題a3とは異なり parse_expression() の返り値の型が Tree *
に変わっていることに注意する．なお，実装した構文解析器が正しく動くかを，
次のプログラムファイルを使って結果を print() で表示して確認する．
・b2.c (構文木の基本操作の利用例)
必要に応じて入力例を追加すること．また，正しい結果が得られない場合は，
構文木の内部構造の表示関数 show_tree() による表示も併用して，
原因を調べること．
●基本課題b3 (式の評価)
評価器(evaluator)は，プログラムの式(を表す構文木)を受け取って，
式の値を求める機能をもつ．SS言語の四則演算を含む算術式の評価関数
eval[・] を，式の構造に沿って次式で再帰的に定義する．
eval[e] = e (e が数のとき)
eval[e] = 1 (e が名前のとき)
eval[(if e1 e2 e3)] = eval[e2] (eval[e1]≠0 のとき)
eval[(if e1 e2 e3)] = eval[e3] (eval[e1]＝0 のとき)
eval[(+ e1 e2)] = eval[e1] + eval[e2]
eval[(- e1 e2)] = eval[e1] - eval[e2]
eval[(* e1 e2)] = eval[e1] * eval[e2]
eval[(/ e1 e2)] = eval[e1] / eval[e2]
eval[(% e1 e2)] = eval[e1] % eval[e2]
※ここで，右辺に現れる算術演算は C 言語の整数演算と同じ意味をもち，
0 での除算は実行時エラーを生じる (C 言語と同様に異常終了してよい)．
変数の値の定義の機能は課題cで扱うので，上記の定義の2行目に示されて
いるように，この課題では，名前を常に 1 と評価する．
例えば，式 (* (+ x 1) 2) を定義に沿って評価した結果は次の通りである．
eval[(* (+ x 1) 2)]
= eval[(+ x 1)] * eval[2]
= (eval[x] + eval[1]) * eval[2]
= (1 + 1) * 2
= 2 * 2
= 4
式の評価を実現するための以下のヘッダとプログラムのファイルを
~/proglang/ に保存する．
・evaluator.h (評価器のヘッダ)
・evaluator.c (評価器のソース)
上記の定義をふまえて，evaluator.c の関数 evaluate() を完成させよ．
実装した評価器が正しく動くことの確認には，次のプログラムファイルを使う．
・b3.c (式の評価)
同様にして，組み込み演算として，比較演算 =, < や論理演算 not, and, or
を含む式の値を評価できるようにせよ．真理値は C 言語と同様に，0 で偽，
0 以外の値 (通常は1) で真を表す．
なお，この課題では，構文木は正しい形の入力プログラムを表していることを
想定してよい．例えば，(if 1) や (* if if) などの誤った形のプロブラムの
構文木に対する誤り処理は，この課題では実装しなくてもよい．
●発展課題b4 (リスト処理)
この課題は必須ではないので，余力のある場合に実施する．
SS言語のデータ式 (data e) は，値を求める際に式 e の部分を評価せず，
式 e をそのままデータとして扱う．
eval[(data e)] = e
例えば，(data (a b c)) は (a b c) というリスト，(data a) は名前 a，
(data (+ 1 2)) は (+ 1 2) というリストへと評価される．
data 式を評価できるように(構文解析器や)評価器を拡張し，リスト処理の
組み込み関数として次のものを扱えるようにせよ．
・リストの空判定 null?
・リストの構成 cons
・リストの先頭要素 head
・リストの先頭要素を取り除いた残りのリスト rest
例えば，(null? (data (a b c d))) と (null? (data ())) の評価結果は
それぞれ 0 と 1，(cons 1 (data (2 3))) はリスト (1 2 3) となる．
また，(head (data ((X) (Y) (Z)))) と (rest (data ((X) (Y) (Z))))
の評価結果は (X) と ((Y) (Z)) となる．
ただし，(null? e)，(cons x e), (head e), (rest e) の e として
数や名前が与えられた場合は，この課題では実行時エラーとする
(課題cで名前がリストに評価される場合は正しく評価できるようになる)．
head, rest の e が空リストとなる場合や，(+ 0 (data ())) など
数の演算にリストが与えられた場合も実行時エラーとする．
●発展課題b5 (構文木の改良)
この課題は必須ではないので，余力のある場合に実施する．
構文木のデータ構造に効率を改善するための工夫を加えたり，
課題b1で指定した以外の方法で実現したりして，計算量の観点での
利点や欠点を論じよ．
余力があれば，データ構造の実装による違いを調べるため，
実行時間や生成ノード数などについて実験的に比較せよ．
実験結果に差が出にくい場合は，大規模な入力例を系統的に作ったり，
評価を多くの回数繰り返したりするとよい．
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
実験のホームページ
山田 俊行
https://www.cs.info.mie-u.ac.jp/~toshi/