━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
課題a (字句解析 と 構文解析)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
●目標
プログラムの文字列を読んで，字句と文法の構造を認識する．
●課題一覧
a1 字句解析
a2 文法と構文解析
a3 構文解析手続きの作成
a4 構文解析の改良
●注意
実験時間内に課題が終わらない場合には，次回に持ち越さずに，
授業以外の時間を使って今回の課題を仕上げておく．
──────────────────────────────────────
●課題aの準備
課題に目を通して，言語処理系の構成と構文解析についての解説に
不明点があれば，自分で調査して基礎知識を事前に補っておく．
ホームディレクトリに proglang という名前のディレクトリを新たに作る．
$ mkdir ~/proglang
このディレクトリを，言語処理系の実験の後半(第4〜7週)の作業場所に使う．
$ cd ~/proglang/
本実験での言語処理系の開発に使う，以下のヘッダとプログラムのファイルを
~/proglang/ に保存する．ファイル名を示した左側のリンクは，ファイルの
保存用であり，内容の説明を示した右側の ( ) 内のリンクは，ブラウザでの
閲覧用である．左右のファイルのコードは同一のものである．
・base.h (基本関数群のヘッダ)
・base.c (基本関数群のソース)
・tokenizer.h (字句解析器のヘッダ)
・tokenizer.c (字句解析器のソース)
ヘッダファイルには，関数の使い方の簡単な説明がある．どんな関数が使える
かを知るために1度は目を通し，後で使うときに必要に応じて参照するとよい．
これらのファイルは，基本課題を実施する際には書き換える必要がないが，
今後，独自の機能を追加したり，発展課題で言語を拡張する際には，
必要に応じて内容を理解した上で変更を加えてもよい．
──────────────────────────────────────
●基本課題a1 (字句解析)
プログラミング言語処理系への入力であるソースプログラムを解析する際，
字句解析器(tokenizer,scanner)によって，文法的に意味のある最小単位である
字句(token)が，入力文字列から一つずつ切り出される．言語処理系は，
字句解析器が認識する字句に応じて，入力の解析の次の動作を決めるので，
使える字句の種類を知っておくことが重要である．
まず，字句解析器の役目や利用方法を理解するための次のソースファイルを
~/proglang/ に保存する．
・a1.c (字句解析の利用例のソース)
・Makefile (課題a用のMakefileの例)
プログラム a1.c を使って，次のコマンドで字句解析の実行ファイルを作る．
$ gcc -c base.c -o base.o
$ gcc -c tokenizer.c -o tokenizer.o
$ gcc -c a1.c -o a1.o
$ gcc base.o tokenizer.o a1.o -o a1
上記の Makefile を使えば，次のコマンドで実行ファイルをビルドできる．
Makefile は，今後，必要に応じて記述を 編集・追加 して使う．
$ make clean
$ make a1
a1.c のプログラムは未完成なので，未使用の変数についての警告が出ても，
今は気にしなくてよい．
字句解析器により，入力文字列が字句(token)に分割されることを，
次のコマンドで実行して確認する．
$ ./a1
本実験で扱うプログラミング言語は，Lisp 風の単純な構文をもつ
小規模(small size)の言語であり，以後，これをSS言語と呼ぶ．
この言語の字句構文の詳細は SS言語の構文 に定義されているが，
今は，左括弧 "("，右括弧 ")"，数，名前，の4種類の字句があることを
知っていれば十分である．
tokenizer.h の字句解析の関数のうち，a1.c のプログラムに現れる
tokenize() と next_token() の使い方を理解せよ．さらに，
字句の種類も表示できるように，a1.c にコードを書き加えよ．
具体的には，例えば入力の文字列が "(-01234 if [?])" のとき，
字句の種類が次の形式で表示できるように，a1.c 内の関数 print_token()
の手続きを完成させよ．数を表す文字列と数値との違いに特に注意すること．
source: "(-01234 if [?])"
token1: "(" LPAREN
token2: "-01234" NUMBER(-1234)
token3: "if" NAME("if")
token4: "[?]" UNKNOWN
token5: ")" RPAREN
【参考】tokenizer.h の関数一覧．
●基本課題a2 (文法と構文解析)
文法を使うと，言語処理系が扱うプログラムがどんな字句の並びであるかを
定義できる．本実験の最終目標であるSS言語のプログラムを扱う前に，
単純な算術式を構文解析する例を通して，文法による構文定義や，
文法に沿った構文解析の方法について学ぶ．
文法による言語の定義や構文解析器の書き方を理解するための
次のソースファイルを ~/proglang/ に保存する．
・a2.c (構文解析器の例のソース)
このプログラムは，次の文法で定められた算術式の列を受け付ける．
seq -> exp*
exp -> "(" NAME op NUMBER ")"
op -> "+" | "-"
文法は 左辺 -> 右辺 の形をした生成規則の集まりである．
矢印 -> は「左辺から右辺が生成される」ということを表し，
生成規則を使って，左辺の構文単位を右辺により定義する．
なお，右辺に現れる * は(0回以上の)反復を表し，| は選択を表す．
つまり，上の文法は，列(seq)とは式の0個以上の並びであり，
式(exp)とは "(" 数 演算子 名前 ")" の並びであり，演算子(op)とは
"+" か "-" である，という規則を定める．
プログラミング言語処理系の構文解析器(parser)は，プログラムの構文を
検査する．文法的に正しいプログラムに対しては，字句解析器が出力した
字句列を生成規則に従ってまとめ，後の解析処理に必要な場合には，
木構造の中間データを生成する．a2.c のプログラムを生成規則と
対応させて読み，文法に沿って構文解析器を作る方法を理解せよ．
本実験で採用する再帰下降型の構文解析器(recursive descent parser)では，
文法の各左辺に1つずつ解析手続を対応させる．各解析手続きは，対応する
規則の右辺の構造に沿って作り，規則の選択 | は条件文で，規則の反復 *
は反復文で構文解析の処理を書く．規則の右辺に字句が現れる場所では，
字句解析で得られた入力字句を生成規則の字句と照合する．照合に成功すれば
その字句の処理と次の字句の読み込みをし，失敗すれば誤り処理をする．
また，右辺に左辺の記号が現れる場所では，対応する解析手続きを呼び出す．
a2.c のプログラムから実行ファイルをビルドして実行すると，
構文解析の手続きの実行中に認識された字句が順に表示される．
上記の算術式列の文法に沿った入力例としては "(ab + 12) (cde - 345)"
が挙げられる．この文字列は，字句解析により次の字句の列に分割される．
"(" NAME "+" NUMBER ")" "(" NAME "-" NUMBER ")"
文法に沿った字句列は，生成規則の左辺と右辺の関係を親子関係，
右辺の並びを兄弟関係とする木構造でも表せる．これを解析木と呼ぶ．
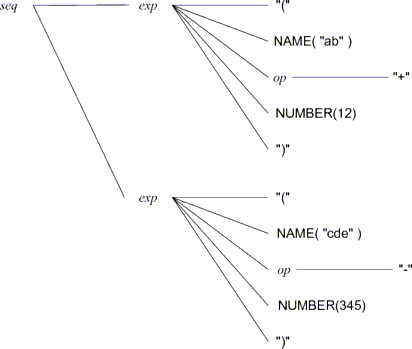なお，解析手続きの実行時の出力と対応させやすいように，ここでは，
解析木の親子の節を左から右へ，兄弟の節を上から下へと並べて示す．
構文解析の手続きの呼び出しと復帰や字句の処理は，解析木の節を
深さ優先探索で訪問する順に進む．上の例での処理順は次の通りである．
seq始 exp始 "(" NAME("ab") op始 "+" op終 NUMBER(12) ")" exp終 exp始 …
プログラム a2.c の各解析手続きの先頭と末尾にある表示処理を有効にして，
構文解析の手続きの呼び出しと復帰の順も表示するプログラムを作る
ことで，解析木の節の走査順との対応を調べよ．たとえば，入力文字列が
"(x + 0)" のとき，次の出力できればよい．
source: "(x + 0)"
[seq
[exp(x[op+op]0)exp]
seq]
また，構文誤りがある時の例をいくつか作って構文解析を実行し，
適切な解析位置で誤りが検出されることを確かめよ．
【参考】再帰下降型の構文解析
●基本課題a3 (構文解析手続きの作成)
本実験の目標であるプログラミング言語処理系の構文解析手続きを作る．
SS言語の式(expression)の文法は，次の生成規則で定義される．
expression -> NUMBER | NAME | "(" expression* ")"
この文法は，expression の定義中に expression が現れる，再帰的な文法で
あることに注意する．これは，式の中に一段階小さな部分式が現れる
ことに対応する．
この言語が扱うプログラムの例を以下に示す．
(and (< 10 20) (or (not (< 30 40)) (= 50 60)))
(+ (- 100 200) (% (/ (* 300 400) 500) 600))
(def x -100)
(def y -200)
(if (< x y) x y)
基本課題では，算術演算や論理演算を使った式，変数定義，条件式を扱える．
発展課題で言語を拡張すれば，例えば次のプログラムを解釈し実行できる．
最小値，最小公倍数，リストの連結，の関数を定義して使うプログラムである．
(fun (min x y) (if (< x y) x y))
(min -100 -200)
(fun (gcd m n) (if (= n 0) m (gcd n (% m n))))
(gcd 60 42)
(fun (append l1 l2) (if (null? l1) l2 (cons (head l1) (append (rest l1) l2))))
(append (data (a b c)) (data (d e f)))
a2.c の構文解析プログラムを参考にして，上記の文法の式(expression)
の構文解析関数 parse_expression() をプログラムファイル a3.c に作れ．
構文解析によって文法の階層構造が正しく認識できることを，
プログラムを作り，複数の入力例を使って確かめよ．
ただし，a3.c に書いた構文解析関数を使って，文法の規則による
左辺から右辺への生成の回数に応じた字下げをして表すプログラムを
a3.c に作ること．たとえば，入力文字列が "(if (< x 0) (- 0 x) x)"
のとき，次の出力できればよい．
source: "(if (< x 0) (- 0 x) x)"
(
if
(
<
x
0
)
(
-
0
x
)
x
)
【参考】a2.c の構文解析手続き，第2,3週で使った木の表示手続き．
●発展課題a4 (構文解析の改良)
この課題は必須ではないので，余力のある場合に実施する．
課題a3で扱った式の文法は，構文解析を単純化するため，本実験で扱う言語の
プログラムとして誤りのある式も生成できてしまう．
例えば，SS言語の文法 の処理系向けの文法で定義された
条件式は (if 式 式 式) の形であるが，課題a3の構文解析器では，
(if 0) などの誤りのある式も受け付けてしまう．
構文解析の段階で構文誤りを検出できるように，処理系向けの文法を
再帰下降型の構文解析に適した形に等価変換せよ．再帰下降型の構文解析器を
作りやすくするには，文法を等価変換して「先読み字句により，どの規則の
どの位置の解析動作を実行するかが一意に決まる」という性質をもつ形
(LL(1)文法)に書き換えておくことが重要である．
変換後の文法に沿った誤り処理ができる構文解析器をファイル a4.c に作って，
a3.c の構文解析器では検出できなかったどんな構文誤りが検出できるように
なったかを，具体的な入力例とそれに対応する実行結果を使って説明せよ．
余力があれば，error_exit() に渡す文字列を変えて，誤りの原因が分かる
ように工夫したり，字句解析器や構文解析器の機能を拡張して，誤りの位置を
表示できるようにするとよい．
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
実験のホームページ
山田 俊行
https://www.cs.info.mie-u.ac.jp/~toshi/