━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
計算量の関数 と 実行時間
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━

次のグラフは，計算量を表す関数と実行時間との関係を表している．



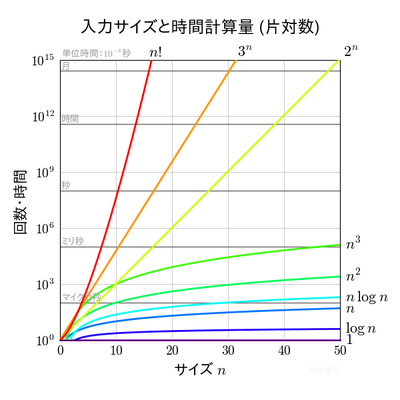
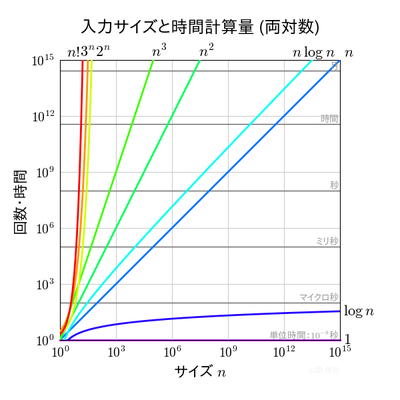基本単位の処理の総回数を，問題のサイズ n の関数 f(n) で表す．
グラフには，基本単位の実行時間を 1/10^8 秒 (10ナノ秒) と想定したときの，
基本処理 f(n) 回の総実行時間が示されている．

横軸の問題のサイズ n は，左のグラフでは線形目盛り，右のグラフでは対数目盛り，
縦軸の回数や時間 f(n) は，二つのグラフとも対数目盛りである．
このため，左のグラフでは，指数関数が直線となることに注意する．

左のグラフでは，指数的に値が増える関数は左上にあり，サイズが n＝50 でも，
処理時間が1か月を超える．一方，多項式時間の関数は右下にあり，
問題のサイズが増えるときに実行時間が比較的緩やかに増える．
右のグラフから分かるように，計算量が多項式時間の関数であっても，
大規模な問題に対して，現実的な時間内に計算できるものは限られる．

なお，単位時間がここでの想定の1000倍(＝10^3倍)に変われば，
時間の太線の目盛り(秒，時間，月 など)は細線の1目盛り分だけ下へ平行移動し，
1000分の1(＝10^(-3)倍)になれば1目盛り上に移動する．

━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
授業のホームページ

山田 俊行
https://www.cs.info.mie-u.ac.jp/~toshi/