━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
課題1 (2分木のデータ構造)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
●準備
次のファイルを,ディレクトリ ~/AdvProg/T6/ に保存しておく.
tree.h
2分木のデータと基本関数のためのヘッダ
tree.c
2分木の基本関数
ex1.c
課題1解答用ひな型
Makefile
自動コンパイル用
予習時に上記のソースファイルと以下の課題を熟読し,疑問点を明らかにしておく.
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
●課題一覧
基本課題
1a 2分木データの生成と表示
1b 2分木を扱う再帰関数の作成
1c 2分木のデータ構造の理解
発展課題
1d 2分木に関する判定
1e 2分木の加工
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
●基本課題 1a (2分木データの生成と表示)
2分木の節を格納するためのデータ構造 (Tree 型) が,2分木のデータと基本関数の
ヘッダファイル tree.h で,次のように定義されている.
typedef struct _tree {
char node; /* 節のデータ (1文字) */
struct _tree *left; /* 左の子へのポインタ */
struct _tree *right; /* 右の子へのポインタ */
} Tree;
 2分木の枝と葉のデータを生成するための二つの関数 branch() と leaf() を作れ.
2分木の基本関数のプログラムファイル tree.c にある定義を,以下の説明に沿って
完成させること.
Tree *branch(char x, Tree *l, Tree *r);
・節 (Tree 型の構造体) を格納する記憶領域を確保
・節を初期化 (節データを x,左右の子へのポインタを l, r に設定)
・生成した Tree 型の構造体へのポインタを戻り値として返却
2分木の枝と葉のデータを生成するための二つの関数 branch() と leaf() を作れ.
2分木の基本関数のプログラムファイル tree.c にある定義を,以下の説明に沿って
完成させること.
Tree *branch(char x, Tree *l, Tree *r);
・節 (Tree 型の構造体) を格納する記憶領域を確保
・節を初期化 (節データを x,左右の子へのポインタを l, r に設定)
・生成した Tree 型の構造体へのポインタを戻り値として返却
 Tree *leaf(char x);
・節 (Tree 型の構造体) を格納する記憶領域を確保
・節を初期化 (節データを x,左右の子へのポインタを NULL に設定)
・生成した Tree 型の構造体へのポインタを戻り値として返却
Tree *leaf(char x);
・節 (Tree 型の構造体) を格納する記憶領域を確保
・節を初期化 (節データを x,左右の子へのポインタを NULL に設定)
・生成した Tree 型の構造体へのポインタを戻り値として返却
 これ以降の課題の答えは,課題1のソースファイル ex1.c に書き込む.
関数 branch() と leaf() を使って,算術式を表す2分木のデータを生成し,
各2分木の根へのポインタを,Tree * 型の変数に格納せよ.
例えば,算術式
0
a + b
(x + (y + 1)) * z
を表すデータを作るなら,それぞれ,次の図の2分木を生成する.
これ以降の課題の答えは,課題1のソースファイル ex1.c に書き込む.
関数 branch() と leaf() を使って,算術式を表す2分木のデータを生成し,
各2分木の根へのポインタを,Tree * 型の変数に格納せよ.
例えば,算術式
0
a + b
(x + (y + 1)) * z
を表すデータを作るなら,それぞれ,次の図の2分木を生成する.

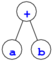
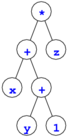 ファイル tree.c で定義された関数 show_tree() の処理内容を理解した上で,
この関数を使って2分木を表示し,意図通りのデータができていることを確かめよ.
補足
●基本課題 1b (2分木を扱う再帰関数の作成)
2分木の高さを求める関数 height() を作れ.
ここでの木の高さは,根から葉へたどるときに通る頂点数の最大値,と定義する.
例えば,課題 1a の三つの2分木の高さは,それぞれ 1, 2, 4 である.
十分な数の検査データを作り,動作の正しさを確かめよ.
補足
●基本課題 1c (2分木のデータ構造の理解)
まず,次の2分木のデータを生成するプログラムを作る.
ファイル tree.c で定義された関数 show_tree() の処理内容を理解した上で,
この関数を使って2分木を表示し,意図通りのデータができていることを確かめよ.
補足
●基本課題 1b (2分木を扱う再帰関数の作成)
2分木の高さを求める関数 height() を作れ.
ここでの木の高さは,根から葉へたどるときに通る頂点数の最大値,と定義する.
例えば,課題 1a の三つの2分木の高さは,それぞれ 1, 2, 4 である.
十分な数の検査データを作り,動作の正しさを確かめよ.
補足
●基本課題 1c (2分木のデータ構造の理解)
まず,次の2分木のデータを生成するプログラムを作る.
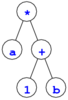 Tree *t1, *t2, *t3;
t1 = leaf('a');
t2 = branch('+', leaf('1'), leaf('b'));
t3 = branch('*', t1, t2);
2分木の節の内容を詳細表示する関数 show_node() を使って,
t1, t2, t3 が指す節が記憶領域上でどのように格納されるかを調べよ.
また,Tree 型 (つまり struct _tree 型) と,その構成要素である
char 型,Tree * 型,それぞれの型のデータの記憶に必要なバイト数を,
sizeof(Tree), sizeof(char), sizeof(Tree *),の値を表示して調べよ.
この実行結果をもとに (必要なら他の追加実験をして),
2分木全体が記憶領域上でどのように格納されるかを説明 (図解) せよ.
補足
──────────────────────────────────────
●発展課題 1d (2分木に関する判定)
与えられた2分木が左右対称かどうかを判定する関数 is_symmetric() を作れ.
例えば,算術式 x や (y + 1) * (1 + y) を表す木
Tree *t1, *t2, *t3;
t1 = leaf('a');
t2 = branch('+', leaf('1'), leaf('b'));
t3 = branch('*', t1, t2);
2分木の節の内容を詳細表示する関数 show_node() を使って,
t1, t2, t3 が指す節が記憶領域上でどのように格納されるかを調べよ.
また,Tree 型 (つまり struct _tree 型) と,その構成要素である
char 型,Tree * 型,それぞれの型のデータの記憶に必要なバイト数を,
sizeof(Tree), sizeof(char), sizeof(Tree *),の値を表示して調べよ.
この実行結果をもとに (必要なら他の追加実験をして),
2分木全体が記憶領域上でどのように格納されるかを説明 (図解) せよ.
補足
──────────────────────────────────────
●発展課題 1d (2分木に関する判定)
与えられた2分木が左右対称かどうかを判定する関数 is_symmetric() を作れ.
例えば,算術式 x や (y + 1) * (1 + y) を表す木

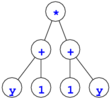 は対称的だが,a * 1 や (a * 1) + (1 + a) を表す木
は対称的だが,a * 1 や (a * 1) + (1 + a) を表す木
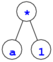
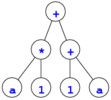 は対称的ではない.
補足
●発展課題 1e (2分木の加工)
2分木を左右反転した鏡像を求める関数 mirror() を作れ.
例えば,(a * b) * (1 + x) の2分木に対して (x + 1) * (b * a) の2分木
が得られればよい (下図).
は対称的ではない.
補足
●発展課題 1e (2分木の加工)
2分木を左右反転した鏡像を求める関数 mirror() を作れ.
例えば,(a * b) * (1 + x) の2分木に対して (x + 1) * (b * a) の2分木
が得られればよい (下図).
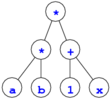 →
→ 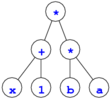 補足
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
演習のホームページ
山田 俊行
https://www.cs.info.mie-u.ac.jp/~toshi/
補足
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
演習のホームページ
山田 俊行
https://www.cs.info.mie-u.ac.jp/~toshi/
 2分木の枝と葉のデータを生成するための二つの関数 branch() と leaf() を作れ.
2分木の基本関数のプログラムファイル tree.c にある定義を,以下の説明に沿って
完成させること.
Tree *branch(char x, Tree *l, Tree *r);
・節 (Tree 型の構造体) を格納する記憶領域を確保
・節を初期化 (節データを x,左右の子へのポインタを l, r に設定)
・生成した Tree 型の構造体へのポインタを戻り値として返却
2分木の枝と葉のデータを生成するための二つの関数 branch() と leaf() を作れ.
2分木の基本関数のプログラムファイル tree.c にある定義を,以下の説明に沿って
完成させること.
Tree *branch(char x, Tree *l, Tree *r);
・節 (Tree 型の構造体) を格納する記憶領域を確保
・節を初期化 (節データを x,左右の子へのポインタを l, r に設定)
・生成した Tree 型の構造体へのポインタを戻り値として返却
 Tree *leaf(char x);
・節 (Tree 型の構造体) を格納する記憶領域を確保
・節を初期化 (節データを x,左右の子へのポインタを NULL に設定)
・生成した Tree 型の構造体へのポインタを戻り値として返却
Tree *leaf(char x);
・節 (Tree 型の構造体) を格納する記憶領域を確保
・節を初期化 (節データを x,左右の子へのポインタを NULL に設定)
・生成した Tree 型の構造体へのポインタを戻り値として返却
 これ以降の課題の答えは,課題1のソースファイル ex1.c に書き込む.
関数 branch() と leaf() を使って,算術式を表す2分木のデータを生成し,
各2分木の根へのポインタを,Tree * 型の変数に格納せよ.
例えば,算術式
0
a + b
(x + (y + 1)) * z
を表すデータを作るなら,それぞれ,次の図の2分木を生成する.
これ以降の課題の答えは,課題1のソースファイル ex1.c に書き込む.
関数 branch() と leaf() を使って,算術式を表す2分木のデータを生成し,
各2分木の根へのポインタを,Tree * 型の変数に格納せよ.
例えば,算術式
0
a + b
(x + (y + 1)) * z
を表すデータを作るなら,それぞれ,次の図の2分木を生成する.


 ファイル tree.c で定義された関数 show_tree() の処理内容を理解した上で,
この関数を使って2分木を表示し,意図通りのデータができていることを確かめよ.
補足
●基本課題 1b (2分木を扱う再帰関数の作成)
2分木の高さを求める関数 height() を作れ.
ここでの木の高さは,根から葉へたどるときに通る頂点数の最大値,と定義する.
例えば,課題 1a の三つの2分木の高さは,それぞれ 1, 2, 4 である.
十分な数の検査データを作り,動作の正しさを確かめよ.
補足
●基本課題 1c (2分木のデータ構造の理解)
まず,次の2分木のデータを生成するプログラムを作る.
ファイル tree.c で定義された関数 show_tree() の処理内容を理解した上で,
この関数を使って2分木を表示し,意図通りのデータができていることを確かめよ.
補足
●基本課題 1b (2分木を扱う再帰関数の作成)
2分木の高さを求める関数 height() を作れ.
ここでの木の高さは,根から葉へたどるときに通る頂点数の最大値,と定義する.
例えば,課題 1a の三つの2分木の高さは,それぞれ 1, 2, 4 である.
十分な数の検査データを作り,動作の正しさを確かめよ.
補足
●基本課題 1c (2分木のデータ構造の理解)
まず,次の2分木のデータを生成するプログラムを作る.
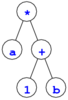 Tree *t1, *t2, *t3;
t1 = leaf('a');
t2 = branch('+', leaf('1'), leaf('b'));
t3 = branch('*', t1, t2);
2分木の節の内容を詳細表示する関数 show_node() を使って,
t1, t2, t3 が指す節が記憶領域上でどのように格納されるかを調べよ.
また,Tree 型 (つまり struct _tree 型) と,その構成要素である
char 型,Tree * 型,それぞれの型のデータの記憶に必要なバイト数を,
sizeof(Tree), sizeof(char), sizeof(Tree *),の値を表示して調べよ.
この実行結果をもとに (必要なら他の追加実験をして),
2分木全体が記憶領域上でどのように格納されるかを説明 (図解) せよ.
補足
──────────────────────────────────────
●発展課題 1d (2分木に関する判定)
与えられた2分木が左右対称かどうかを判定する関数 is_symmetric() を作れ.
例えば,算術式 x や (y + 1) * (1 + y) を表す木
Tree *t1, *t2, *t3;
t1 = leaf('a');
t2 = branch('+', leaf('1'), leaf('b'));
t3 = branch('*', t1, t2);
2分木の節の内容を詳細表示する関数 show_node() を使って,
t1, t2, t3 が指す節が記憶領域上でどのように格納されるかを調べよ.
また,Tree 型 (つまり struct _tree 型) と,その構成要素である
char 型,Tree * 型,それぞれの型のデータの記憶に必要なバイト数を,
sizeof(Tree), sizeof(char), sizeof(Tree *),の値を表示して調べよ.
この実行結果をもとに (必要なら他の追加実験をして),
2分木全体が記憶領域上でどのように格納されるかを説明 (図解) せよ.
補足
──────────────────────────────────────
●発展課題 1d (2分木に関する判定)
与えられた2分木が左右対称かどうかを判定する関数 is_symmetric() を作れ.
例えば,算術式 x や (y + 1) * (1 + y) を表す木

 は対称的だが,a * 1 や (a * 1) + (1 + a) を表す木
は対称的だが,a * 1 や (a * 1) + (1 + a) を表す木

 は対称的ではない.
補足
●発展課題 1e (2分木の加工)
2分木を左右反転した鏡像を求める関数 mirror() を作れ.
例えば,(a * b) * (1 + x) の2分木に対して (x + 1) * (b * a) の2分木
が得られればよい (下図).
は対称的ではない.
補足
●発展課題 1e (2分木の加工)
2分木を左右反転した鏡像を求める関数 mirror() を作れ.
例えば,(a * b) * (1 + x) の2分木に対して (x + 1) * (b * a) の2分木
が得られればよい (下図).
 →
→  補足
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
演習のホームページ
山田 俊行
https://www.cs.info.mie-u.ac.jp/~toshi/
補足
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
演習のホームページ
山田 俊行
https://www.cs.info.mie-u.ac.jp/~toshi/